# 3. 图

3.1 无向图
3.2 有向图
3.3 带权图
3.4 图的表示方式

图是一种复杂的非线性结构。

在树形结构中，数据元素之间有着明显的层次关系，并且每个数据元素只与上一层中的一个元素(parent node)及下一层的多个元素(孩子节点)相关。

在图形结构中，节点之间的关系是任意的，图中任意两个数据元素之间都有可能相关。

图中的节点也被称作顶点（vertice）
两个节点相连的部分称为边（edge）

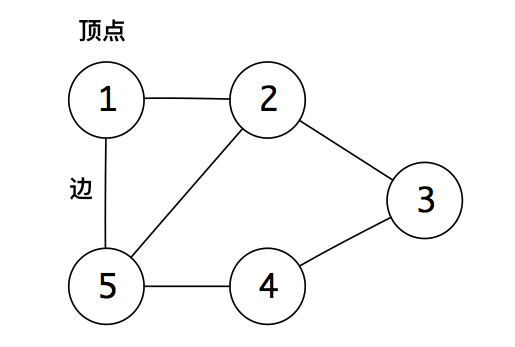
G = (V，E)

# 3.1 无向图

对于一个图，若每条边都是没有方向的，则称该图为无向图。

(Vi，Vj) 和 (Vj，Vi) 表示的是同一条边。

无向图的顶点集和边集分别表示为：

V(G) = {V1，V2，V3，V4，V5}

E(G) = {(V1，V2)，(V1，V4)，(V2，V3)，(V2，V5)，(V3，V4)，(V3，V5)，(V4，V5)}

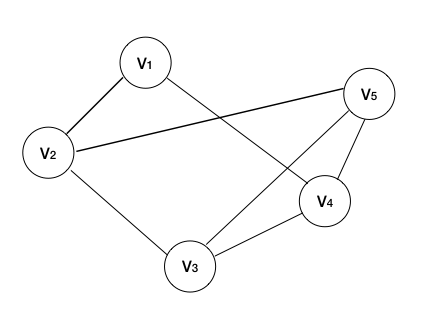
顶点的度

顶点的度表示以该顶点作为一个端点的边的数目（当前顶点有几条边跟它连接）

eg: D(V3) = 3

路径和回路

从一个顶点到另一顶点途径的所有顶点组成的序列（包含这两个顶点）

eg: r = v1, v2, v3

如果路径中第一个顶点和最后一个顶点相同，则此路径称为"回路"（或"环"）

eg: c = v1, v2, v3, v1

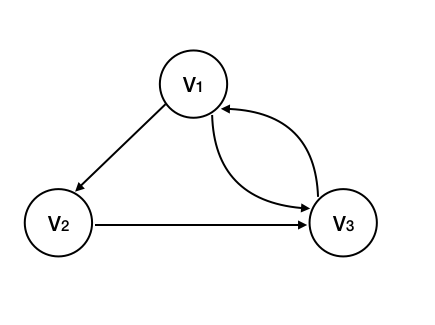
# 3.2 有向图

对于一个图，若每条边都是有方向的，则称该图为有向图。

<Vi，Vj> 和 <Vj，Vi> 是两条不同的有向边。

注意

无向图是用小括号表示，而有向图是用尖括号表示
有向边又称为弧

有向图的顶点集和边集分别表示为：

V(G ) = {V1，V2，V3}

E(G) = {<V1，V2>，<V2，V3>，<V3，V1>，<V1，V3>}

1
2
3

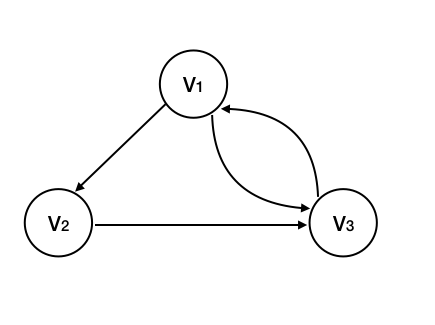
有向图的度

顶点的度分为入度和出度。入度表示以该顶点为终点的入边数目（接收），出度是以该顶点为起点的出边数目（发送），该顶点的度等于其入度和出度之和。

比如，顶点 V1 的入度 ID(V1) = 1，出度 OD(V1) = 2，所以 D(V1) = ID(V1) + OD(V1) = 3

# 3.3 带权图

权（Weight）：图中边和弧有相关的数字，这个数字叫做权（Weight）。

这些带权的图通常称为网（Network）。

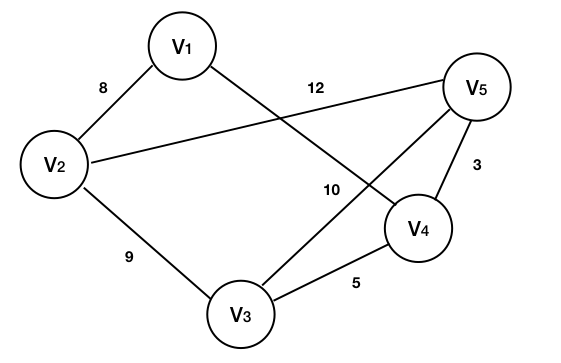
地图应用：

顶点：城市
边：两个城市之间的路线
权重：两个城市之间的距离

# 邻接矩阵

可以使用一个二维数组建立一个矩阵，矩阵元素 a[i] [j]，矩阵横坐标表示起始顶点，纵坐标表示到达顶点。

如果是带权图，矩阵中存储权重，如果顶点直接无关联可以用 ∞ 符号来表示。

const graph = [
  [0, 2, '∞', 5],
  ['∞', 0, '∞', 1],
  [3, '∞', 0, 8],
  ['∞', '∞', '∞', 0],
];

const graph = [
  [1, 1, 0, 1],
  [0, 1, 0, 1],
  [1, 0, 1, 1],
  [0, 0, 0, 1],
]

1
2
3
4
5
6
7
8
9
10
11
12
13

# 邻接表

每个顶点都有一个记录着与它所相邻顶点的表。

可以使用一个数组或者 Map 来建立一个邻接表，它存储这所有的顶点。每个顶点都有一个列表（可以是数组、链表、集合等数据结构），存放着与其相邻的顶点。

const graph = {
  	'v1': [ 'v2'，'v3' ],
  	'v2': [ 'v3' ],
  	'v3': [ 'v1' ],
};

const graph = {
  	'v1': [{ vertice: 'v2', weight: 2 }, { vertice: 'v3', weight: 4 }],
  	'v2': [ 'v3' ],
  	'v3': [ 'v1' ],
};

1
2
3
4
5
6
7
8
9
10
11

# 图论

图论（英语：Graph theory），是组合数学的一个分支，和其他数学分支，如群论、矩阵论、拓扑学有着密切关系。图是图论的主要研究对象。图是由若干给定的顶点及连接两顶点的边所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物，连接两顶点的边则用于表示两个事物间具有这种关系。

← 2.5 堆