2.4 并查集

• 2.4.1 并查集的实现

并查集（Union / Find）是一种特殊的树结构，用于处理一些不交集的合并及查询问题。

并查集就是：使用合并和查找的方式来解决集合的问题

初始时并查集中的元素是不相交的，经过一系列的基本操作(Union)，最终合并成一个大的集合

主要用来解决 动态连通性 一类问题的一种算法

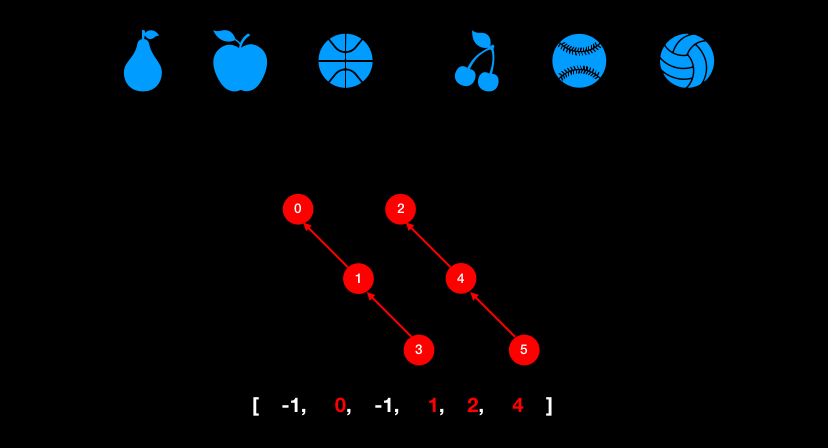
该结构中每个节点都有一个父节点，如果只有当前一个节点，那么该节点的父节点指向自己。

并查集的特点：

1. 树结构是逆向的，子节点指向父节点
2. 森林结构

2.4.1 并查集的实现

这里引入一种新的合并策略，这是一种启发式策略，称之为按秩合并。

秩就是层级

翻译成人话：就是将层级小的子树的根指向层级大的子树的根。

class DisjointSet {
  // 初始化样本
  constructor(count) {
    // 初始化时，每个节点的父节点都是自己
    this.parent = new Array(count);
    // 用于记录树的层级，用于按秩合并
    this.rank = new Array(count);
    for (let i = 0; i < count; i++) {
      this.parent[i] = i;
      this.rank[i] = 1;
    }
  }
  // 算法流程
  // 目的：找到目标节点的根节点 find(3) -> 0
  // 1. 循环判定，当前节点的值（父节点）是否为自己，如果不是的话表示还没找到
  // 2. 则当前节点的值重新赋值，等于以数组项为索引的值
  // 3. 重新赋值后，继续循环判定
  // 4. 直到当前节点的值等于自己，返回当前节点的值

  find(p) {
    while (p != this.parent[p]) {
      this.parent[p] = this.parent[this.parent[p]];
      p = this.parent[p];
    }
    return p;
  }
  // 算法流程
  // 目的：合并两个节点，会根据树的层级大小判定合并策略
  // 1. 首先需要寻找两个数字的父节点  0 <- 1    2 <- 3  union(3, 1)  <=>  union(0, 2)
  // 2. 如果 两个数字相等，直接退出
  // 3. 判定两棵树的层级，层级小的加到层级大的树下面
  // 4. 如果两棵树的层级相等，那么随意合并
  union(p, q) {
    let i = this.find(p);
    let j = this.find(q);
    if (i === j) return;
    if (this.rank[i] < this.rank[j]) {
      this.parent[i] = j;
    } else if (this.rank[i] > this.rank[j]) {
      this.parent[j] = i;
    } else {
      this.parent[j] = i;
      this.rank[i] += 1;
    }
  }
}