2.5 堆

• 2.5.1 堆和二叉搜索树的区别
• 2.5.2 一棵树的数组对象
• 2.5.3 堆的操作
• 2.5.4 最大堆的实现

堆的一个经典的实现是完全二叉树。这样实现的堆称为二叉堆。

完全二叉树：增加了限定条件的二叉树。假设一个二叉树的深度为 n。为了满足完全二叉树的要求，该二叉树的前n - 1 层必须填满，第 n 层的所有的节点都连续集中在最左边。

这种数据结构具有以下两个性质：

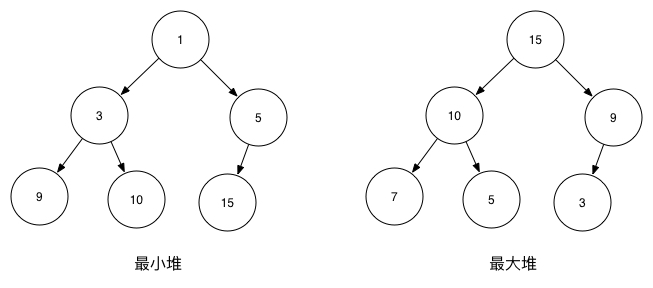
• 堆总是一棵完全二叉树。即除了最底层，其他层的节点都被元素填满，且最底层从左到右填入

• 任意节点小于（或大于）它的所有子节点

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

2.5.1 堆和二叉搜索树的区别

1. 节点的顺序

   在二叉搜索树中，左子节点必须比父节点小，右子节点必须必比父节点大。但是在堆中并非如此。在最大堆中两个子节点都必须比父节点小，而在最小堆中，它们都必须比父节点大。

2. 搜索

   在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行插入、删除操作。

2.5.2 一棵树的数组对象

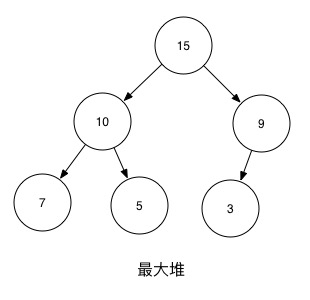
[ 15, 10, 9, 7, 5, 3 ]

节点位置计算公式：

parent(i) = Math.floor((i - 1)/2);
left(i)   = 2i + 1;
right(i)  = 2i + 2;

Node	Index	父节点	左子节点	右子节点
15	0	-1	1	2
10	1	0	3	4
9	2	0	5
7	3	1
5	4	1
3	5	2

2.5.3 堆的操作

插入操作

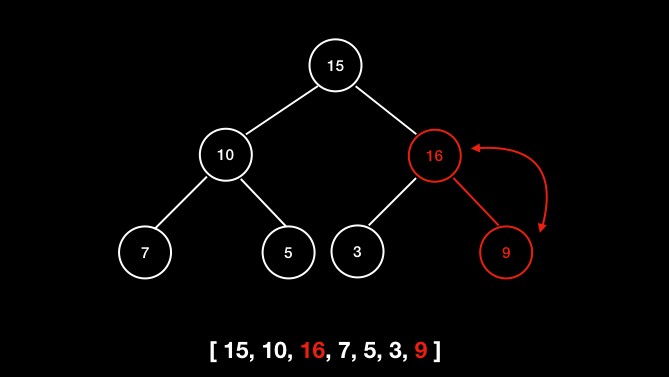
删除根节点

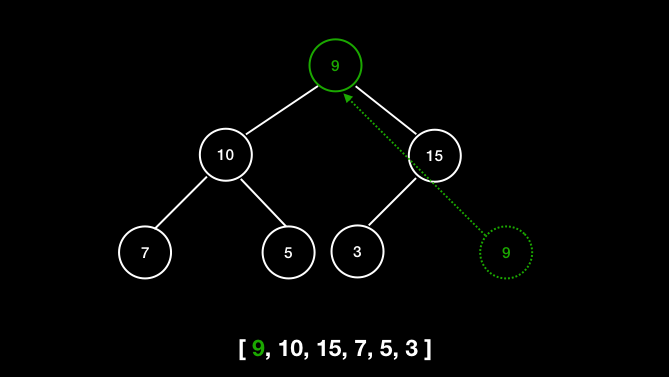
堆有两个核心的操作，分别是 shiftUp 和 shiftDown 。前者用于添加元素，后者用于删除根节点。

shiftUp 的核心思路是一路将节点与父节点对比大小，如果比父节点大，就和父节点交换位置。

shiftDown 的核心思路是先将根节点和末尾交换位置，然后移除末尾元素。接下来循环判断父节点和两个子节点的大小，如果子节点大，就把最大的子节点和父节点交换。

2.5.4 最大堆的实现

class MaxHeap {
  constructor() {
    this.heap = [];
  }

  insert(item) {
    // 将节点直接入队
    this.heap.push(item);
    // 判定是否需要交换位置
    this.shiftUp(this.getSize() - 1);
  }

  remove(index) {
    // 交换位置并且删除队尾节点
    this.swap(index, this.getSize() - 1);
    this.heap.splice(this.getSize() - 1, 1);
    // 判定是否需要交换位置
    this.shiftDown(index);
  }

  getParentIndex(index) {
    return Math.floor((index - 1) / 2);
  }

  getLeftIndex(index) {
    return index * 2 + 1;
  }

  shiftUp(index) {
    // 如果当前节点比父节点大，就交换
    while(this.heap[index] > this.heap[this.getParentIndex(index)]) {
      this.swap(index, this.getParentIndex(index));
      // 将索引修改成父节点
      index = this.getParentIndex(index);
    }
  }

  shiftDown(index) {
    // 判断当前节点是否有左子节点
    while(this.getLeftIndex(index) < this.getSize()) {
      let leftIndex = this.getLeftIndex(index);
      let rightIndex = leftIndex + 1;
      let changeIndex = leftIndex;
      // 判断是否有右子节点，并且右子节点是否大于左子节点
      if (rightIndex < this.getSize() && this.heap[rightIndex] > this.heap[leftIndex]) {
        changeIndex = rightIndex;
      }
      // 判断父节点是否比子节点都大，则终止循环，否则就交换位置
      this.swap(index, changeIndex);
      index = changeIndex;
    }
  }

  swap(left, right) {
    const rightValue = this.heap[right];
    this.heap[right] = this.heap[left];
    this.heap[left] = rightValue;
  }

  getSize() {
    return this.heap.length;
  }

  isEmpty() {
    return this.getSize() === 0;
  }
}