# 2.1 二叉树
二叉树是一种非常重要的数据结构，很多其它数据结构都是基于二叉树的基础演变而来的。
二叉树拥有一个根节点，每个节点至多拥有两个子节点，分别为：左节点和右节点。树的最底部节点称之为叶节点。
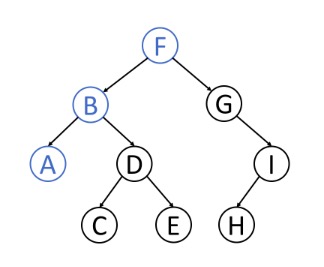
当一颗树的叶数量数量为满时，该树可以称之为满二叉树。
# 2.1.1 二叉树的遍历
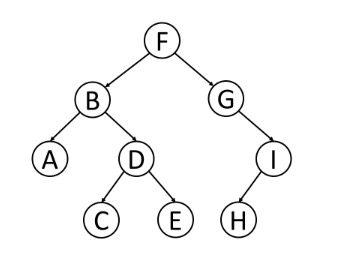
先序遍历--先访问根节点，然后遍历左子树，最后遍历右子树
根 - 左 - 右
F - B - A - D - C - E - G - I - H
中序遍历--先遍历左子树，然后访问根节点，然后遍历右子树
左 - 根 - 右
A - B - C - D - E - F - G - H - I
后序遍历--先遍历左子树，然后遍历右子树，最后访问树的根节点
左 - 右 - 根
A - C - E - D - B - H - I - G - F
这三种遍历也叫做深度优先遍历。
深度优先：把某一边遍历完再说。
// 先序遍历 // 利用栈 var preorderTraversal = function(root) { let myStack = new Stack(); let res = []; root && myStack.push(root); while(myStack.getSize() > 0) { let cur = myStack.pop(); res.push(cur.val); cur.right && myStack.push(cur.right); cur.left && myStack.push(cur.left); } return res; }; // 递归法 var preorderTraversal = function(root) { const res = []; set(root); return res; function set(tree) { if (!tree) return; res.push(tree.val); tree.left && set(tree.left); tree.right && set(tree.right); } };@xc: 代码已经复制到粘贴板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 2.1.2 二叉树的层序遍历
层序遍历（广度优先遍历）就是逐层遍历树结构。
从一个根节点开始，首先访问节点本身。 然后遍历它的相邻节点，其次遍历它的二级邻节点、三级邻节点，以此类推。
F - B - G - A - D - I - C - E - H
F - B - A - D - C - E -G - I - H
// 层序遍历 // 先访问根就对了 var levelOrder = function(root) { const res = []; set(root, 0); return res; function set(tree, count) { if (!tree) return; if (!Array.isArray(res[count])) res[count] = []; res[count].push(tree.val); tree.left && set(tree.left, count + 1); tree.right && set(tree.right, count + 1); } };@xc: 代码已经复制到粘贴板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14